人工智能数学基础与算法可视化实验平台
更新:2025-04-22 16:37:13 点击:
数值模拟技术对于抽象的数学理论的可视化展示具有天然的优势。因此,本公司与河北医科大学医学影像学院数学教研室合作开发了人工智能数学基础与算法可视化实验平台,目前包含日常统计事件与概率、蒙特卡洛方法、数字傅里叶合成器、特征值与特征向量、人工神经网络、贝叶斯计算器与分类器等14个模块。
详情
平台功能:
1. 通过数学实验夯实数学基础、通过常见算法应用实验,掌握基本的算法逻辑与调参方法;
2. 用户可在平台转发实验结果(经管理员认可)形成教学实践的小型社区;
3. 教师或同学可在任何地点(连接网络)上传数据、编辑算法、开展实践教学。
平台模块概览

蒙特卡洛是一个赌场的名字,赌博是典型的随机性事件。蒙特卡洛法是基于随机性思想求解确定性问题的方法,广泛应用于各领域研究中。该模块包括随机投点实现π值求解、不规则区域面积求解以及随机梯度下降法的参数优化等。随机梯度下降法的参数优化模块中,可开放式的调节样本量、迭代次数、迭代因子、参数初始化对最终参数优化结果的影响规律,深入理解AI中所谓样本量、学习率、Epoch、损失函数(loss)、batch size等概念的基础含义。
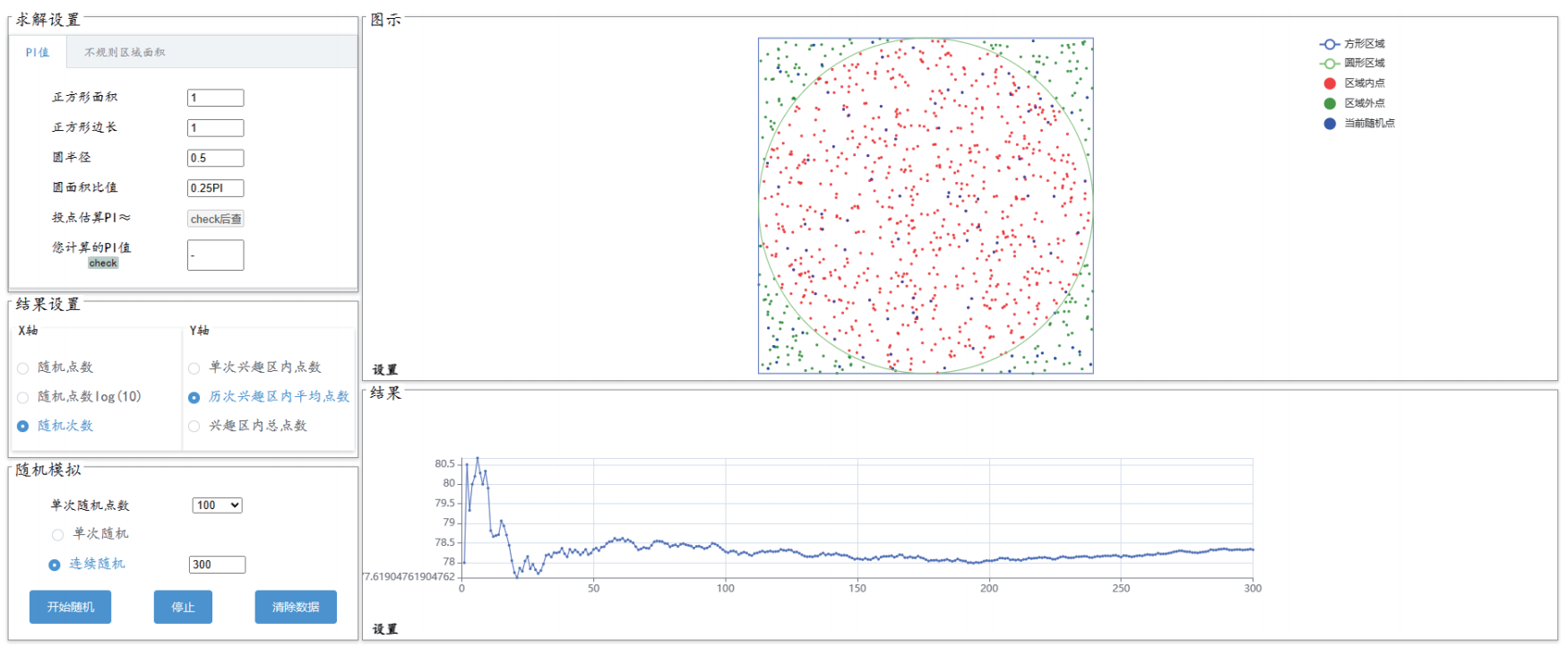
蒙特卡洛方法模块界面
应用于傅里叶函数/级数原理与应用的开放式实验教学,包括基本波形合成、数字音频合成、射频波形调制、心电信号频率分析以及二维傅里叶变换应用等五个部分。从简单的正弦波出发,交互式编辑输入信号,以图像形式输出结果,从而表现时域空间与频域空间的关系;通过调节各种基本参数生成不同的基础波形(三角波、方波、锯齿波等);应用模块包括三个专业领域(音频、心电、核磁)的常见应用。
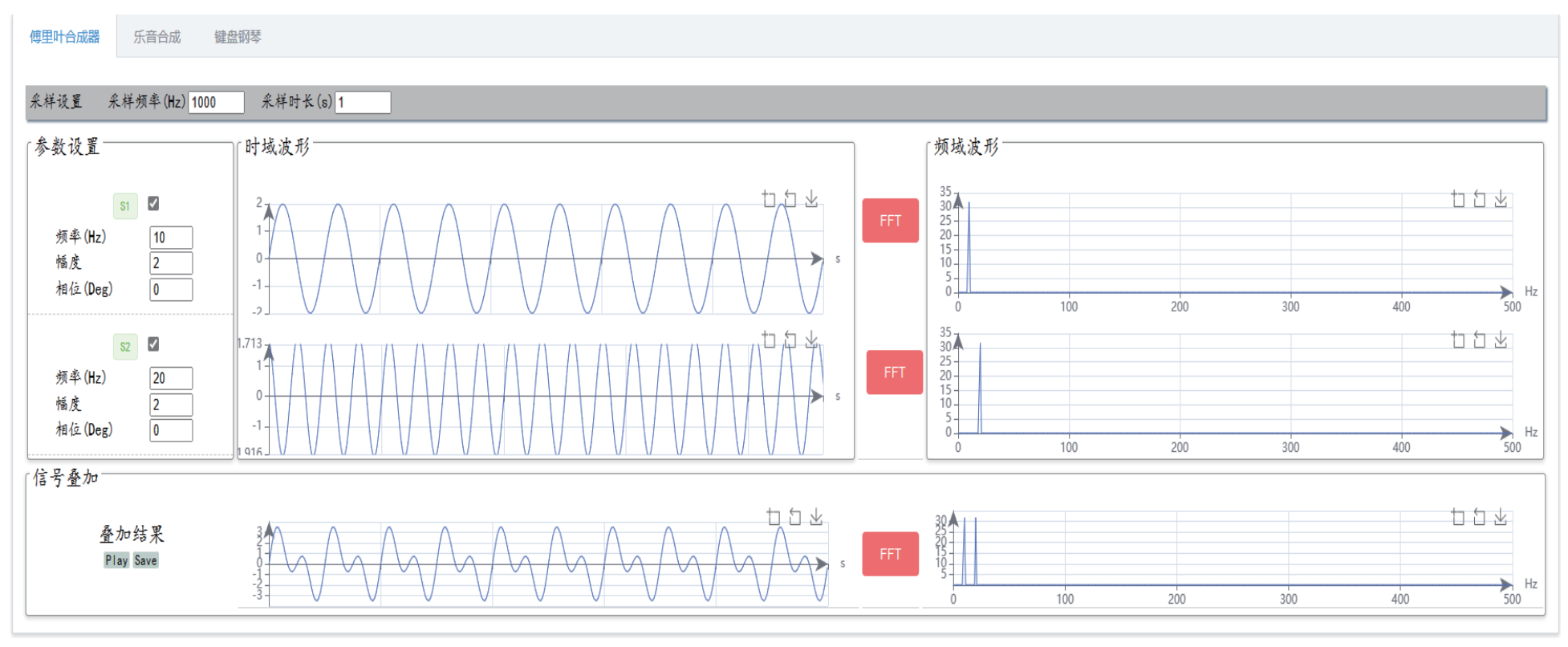
数字傅里叶合成器界面
其他模块:

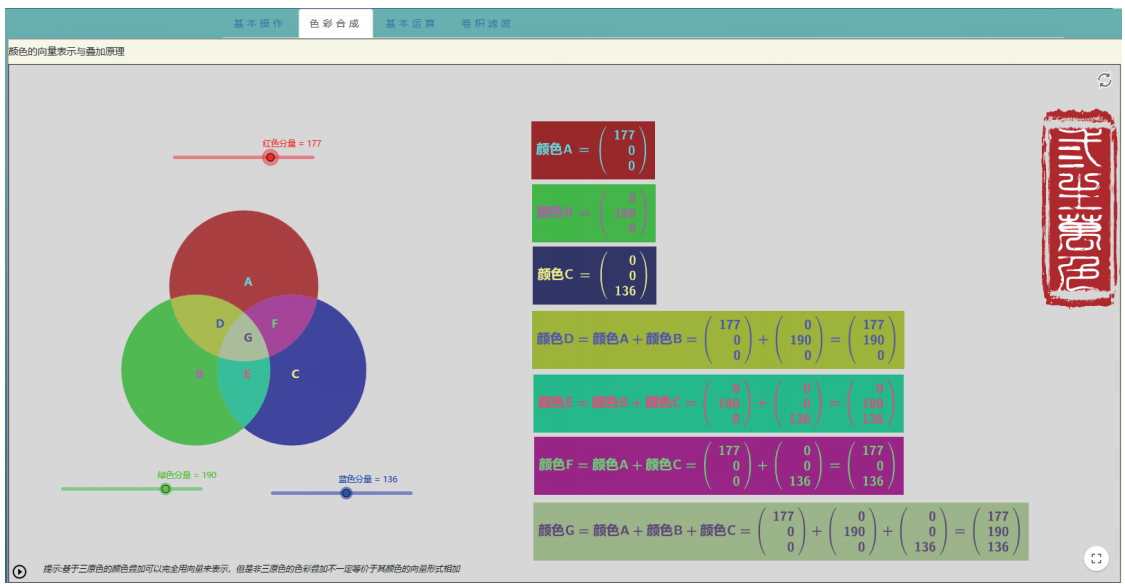
卷积神经网络LeNet5架构 色彩合成界面
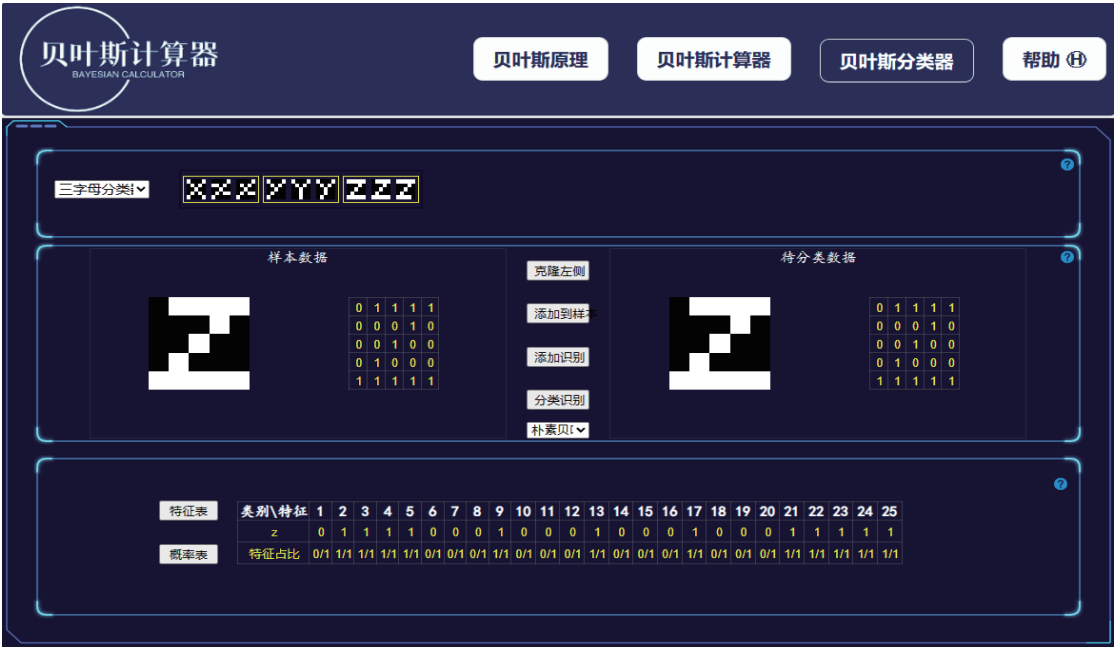
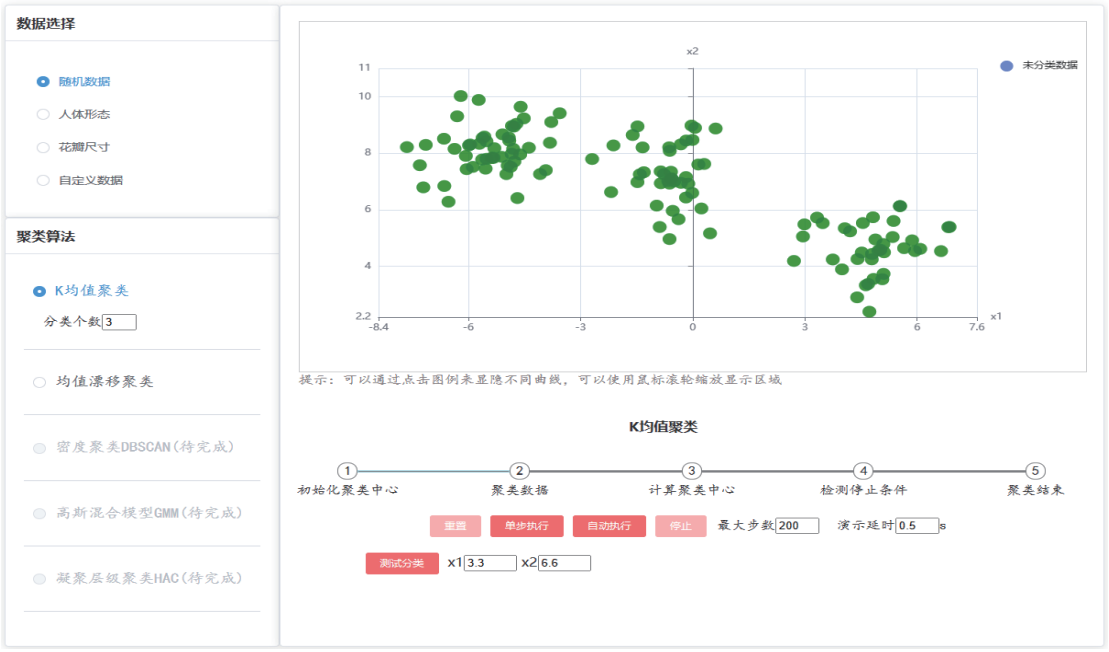
贝叶斯分类器界面 聚类算法界面
相关